Topological Sort

Topological Sort §

The topological sort algorithm takes a directed graph and returns an array of the nodes where each node appears before all the nodes it points to.

Example 1 §

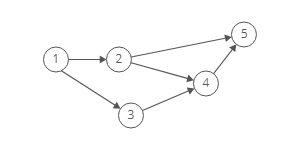
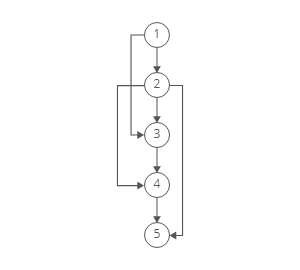
Graphs can have more than one valid topological ordering. This graph has valid ordering of [1,2,3,4,5] or [1,3,2,4,5]

Algorithm §

To produce a topological ordering for this directed graph we have to find the nodes with an Indegree of zero. Nodes with an indegree of zero come first.

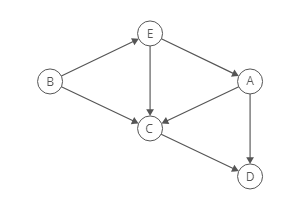
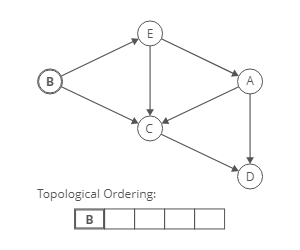
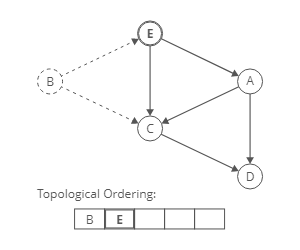
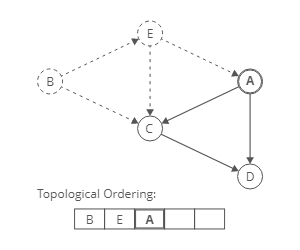
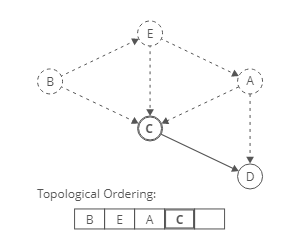
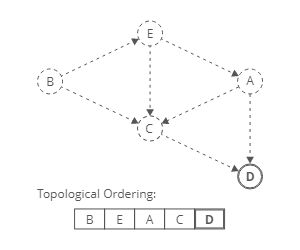
Implementation §

1. Identify a node with no incoming edges.
2. Add that node to the ordering.
3. “Remove” it from the graph by decrementing indegree of neighbours
4. Repeat.

Topological Sort can be useful to find cycles in directed graphs as if a cycle exists there will always be a node with at least one incoming edge.

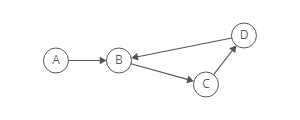
Example §

Leetcode 207 - Course Schedule

Leetcode 207

class Solution {
 
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // Topological sort
        // Prereq array is all the edges
 
		ArrayList<ArrayList<Integer>> nodes = new ArrayList<ArrayList<Integer>>(numCourses);
 
        for (int i = 0; i < numCourses; i++) {
            nodes.add(new ArrayList<Integer>());
        }
 
        int[] degree = new int[numCourses];
  
        // Directed Graph, from edge[1] you can access edge[0]
        for (int[] edge : prerequisites) {
            nodes.get(edge[1]).add(edge[0]);
            degree[edge[0]] += 1; //Increment number of incoming edges
        }
 
        // For you to pass all courses, all courses must be doable
        // Courses cant be all doable if there is a cycle in the graph
        // Therefore there must be a node with zero incoming directed edges
 
        ArrayList<Integer> topSort = new ArrayList<Integer>();
 
        for (int i = 0; i < numCourses; i++) {
            if (degree[i] == 0) {
                topSort.add(i);
            }
        }
 
        for (int i = 0; i < topSort.size(); i++) {
            // Get nodes that are connected to current
            ArrayList<Integer> connectedNodes = nodes.get(topSort.get(i));
            for (int node : connectedNodes) {
                // Now that the current node has been recorded the connected nodes are decremented by a degree of one
                degree[node]--;
                if (degree[node] == 0) {
                    // If they are the degree 0 then that means they are next
                    topSort.add(node);
                }
            }
        }
 
        // If a cycle was detected then the node that creates the cycle would not have been appended
        return (topSort.size() == numCourses);
    }
}

Time Complexity §

Let V be the number of Verticies (nodes) and E be the number of edges

• Time complexity to determine the indegree for each node is O(E) as we must loop over all edges.

• Then we must loop over all nodes and append all that have an indegree of zero to a list/stack. Appending is constant time so this take O(V).

• Then loop over each node in our list/stack, pop off and decrement the connected edges, therefore O(V)

  • Although a loop is used to decrement the edges we won’t count edges twice therefore it has an additional total time complexity of O(E).

Therefore total time complexity is O(V+E).

Space Complexity §

Space complexity is O(V)

• Structure to store the integer number of indegrees for each node is O(V).
• Structure to store all nodes with no incoming edges is O(V) worst case. Worst case all nodes have zero edges
• Topological ordering result is O(V) worst case as all nodes will be in the ordering at the end if the graph has no cycles.

Uses §

• Can be used to find cycles
• Can also be used to find order of a procedure where steps may be dependant on each other
  • E.g baking a cake

References §

https://www.interviewcake.com/concept/java/topological-sort