Box Stacking

Box Stacking Problem §

Leetcode 1691 - Maximum Height by Stacking Cuboids

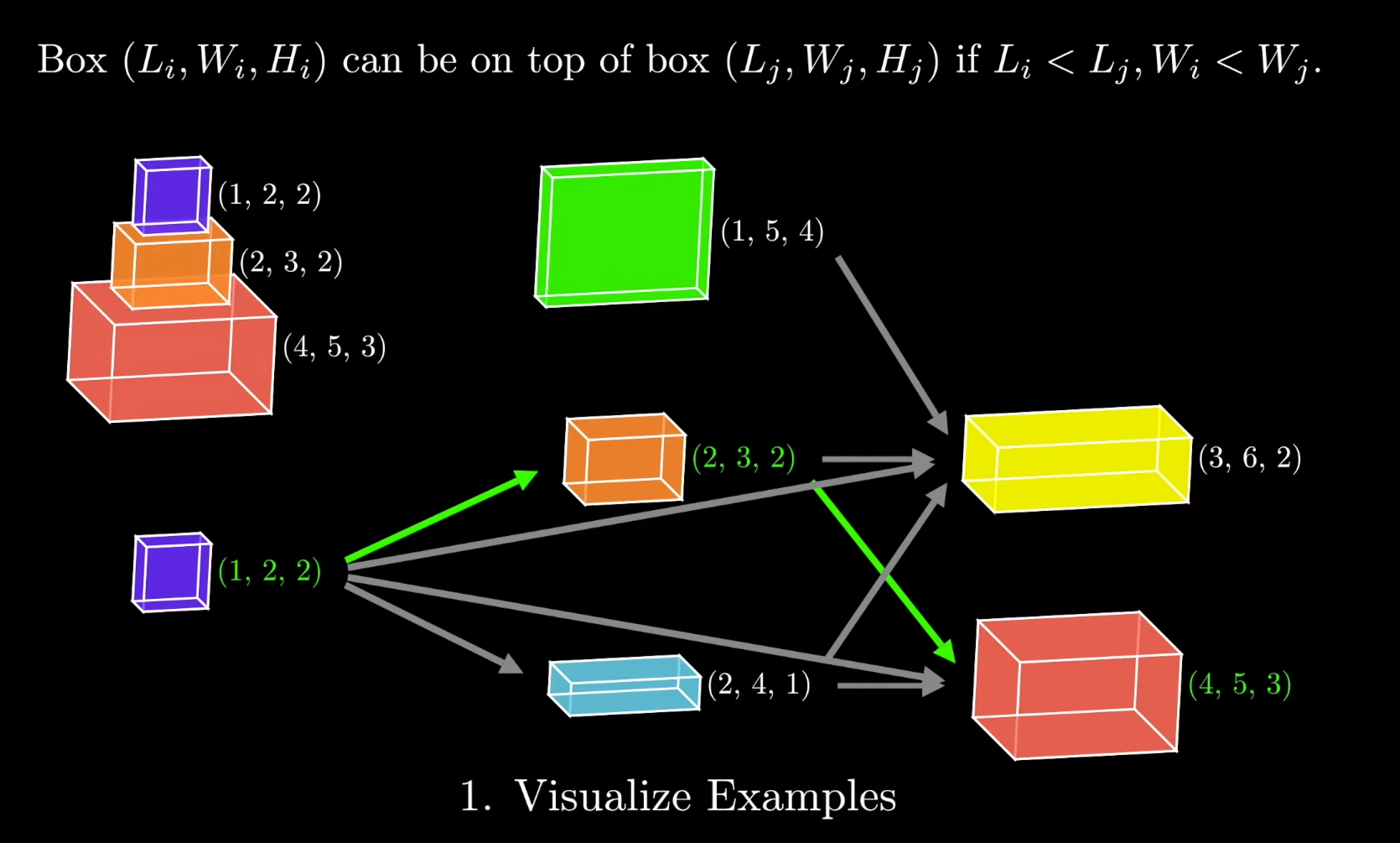
First we can visualise the problem by mapping each box to any box it can be stacked on. Notice that each path in this directed acyclic graph is a valid stack of boxes. To solve this question we need to find the path that gives the greatest height.

Defining the subproblem §

What we know so far:

• A box can only be stacked on another box only when every dimension is greater than or equal to the box its being stacked on
• Each box has a sequence where it is the top or bottom box of the stack

We can describe our subproblem as, max height of stack where box $i$ is at the bottom/base of the stack = $height[(L_i,W_i,H_i)]$

For the image above:

• $height[(2,3,2)]=4$
• $height[(3,6,2)]=6$
• $height[(2,4,1)]=3$

Define the relationship among subproblems §

What subproblems are needed to solve the subproblem for the red box, $height[(4,5,3)]$? The orange, dark blue and cyan boxes can all be stacked on top of the red box. Therefore the subproblems needed are

• $height[(2,3,2)]=4$
• $height[(1,2,2)]=2$
• $height[(2,4,1)]=3$ To find the max height we just add the height of the red box to the tallest height of the other necessary subproblems

$height[(4,5,3)]=3+max\{height[(2,3,2)],height[(1,2,2)],height[(2,4,1)]\}=7$

Generalise the relationship To solve $height[(L_i,W_i,H_i)]$ in general we just need to consider:

• The set of all boxes that can be stacked on top of $(L_i,W_i,H_i)$. Then we can find the max height of stacks that can be made of out this set

Let $S$ be the set of all boxes that can be stacked above $(L_i,W_i,H_i)$ $height[(L_i,W_i,H_i)]=H_i+max\{height[(L_j,W_j,H_j)]|(L_j,W_j,H_j)\in S\}$

Implementation §

To ensure that the optimum height has been computed for each subproblem we need to evaluate the smallest boxes first. We can do this by sorting our input by ascending $(L,W,H)$.

For the Leetcode problem, there is also the added problem of rotating. The boxes can be rotated in order to change its orientation. In order to satisfy the constraint that every dimension needs to be smaller than or equal to the cube its being stacked on, we can sort the cube’s dimensions such that. $\text{small[i] <= small[j] \&\& mid[i] <= mid[j] \&\& large[i] <= large[j]}$

class Solution {
    public int maxHeight(int[][] cuboids) {
        // Sort cubes by size
        for (int [] cube: cuboids) {
            Arrays.sort(cube);
        }
        Arrays.sort(cuboids, new Comparator<int[]>() {
            public int compare(int[] a, int[] b) {
                if (a[0] != b[0])
                    return b[0] - a[0];
                if (a[1] != b[1])
                    return b[1] - a[1];
                return b[2] - a[2];
            }
        });
 
        int[] height = new int[cuboids.length];
        int maxStackHeight = 0;
        for (int i = 0; i < cuboids.length; i++) {
            int[] box = cuboids[i];
            int stackHeight = 0;
            // Compare to all cubes smaller than the current
            for (int j = 0; j < i; j++) {
                if (canStack(box, cuboids[j])) {
                    stackHeight = Math.max(stackHeight, height[j]);
                }
            }
            height[i] = box[2] + stackHeight;
            maxStackHeight = Math.max(maxStackHeight, height[i]);
        }
        return maxStackHeight;
    }
    
    // Can box1 be stacked on box2
    public boolean canStack(int[] box1, int[] box2) {
        return box1[0] <= box2[0] && box1[1] <= box2[1] && box1[2] <= box2[2];
    }
}