Dynamic Programming

Dynamic Programming §

The main idea is to solve a large problem recursively by building from carefully chosen subproblems of smaller size. It is often characterised by overlapping subproblems.

A dynamic programming algorithm consists of three main parts:

1. A definition of the subproblems
2. A recurrence relation, which determines how the solutions to smaller subproblems are combined to solve a larger subproblem
3. Any base cases, which are the trivial subproblems - those for which the recurrence is not required

Structure to solve DP problems:

1. Identify Category: These are the most common categories for DP problems. Being able to identify which one your problem belongs to will help us recall questions we know how to solve.

• 0-1 Knapsack Problem
• Unbounded Knapsack
• Shortest Path (eg: Unique Paths I/II)
• Fibonacci Sequence (eg: House Thief, Jump Game)
• Longest Common Substring/Subsequence

2. States

In terms of Dynamic Programming, a state is defined by a number of necessary variables at a particular instant that are required to calculate the optimal result. So, basically it is a combination of variables that will keep changing over different instants. More the number of states, more is the depth of the recursive solution and more is the memory required to cache the result of the states to avoid re-computing. This is because, you are most likely to have the same state at some point later. Two states are same, if all their corresponding variables have the same logical value. Therefore, it very well makes sense to preserve the results of the state to save time. This gives rise to what is known as Dynamic Programming.

3. Define Subproblem

• Define what subproblem we need to solve and what associates States are required
  • Helps to work out what the answer to each subproblem is in a provided example to visualise the decisions needed
• What decision do I need to make in order at each recursive call?
  • Decisions must bring us closer to the base case
• Generalise these decisions into a recurrence relation.

4. Base Cases

• Base cases need to relate directly to the conditions required by the answer we are seeking. This is why it is important for our decisions to work towards our base cases, as it means our decisions are working towards our answer.

Longest Increasing Subsequence §

Leetcode 300 - Longest Increasing Subsequence First we try to visualise the problem. A common model that can be applied to DP problems is the Directed Acyclic Graph. In this case a directed edge is constructed from one node to the other if the node on the right contains a larger value. An increasing subsequence is just multiple paths in the graph while the Longest Increasing subsequence is the length of the longest path in this DAG + 1 (include the current node as part of the length).

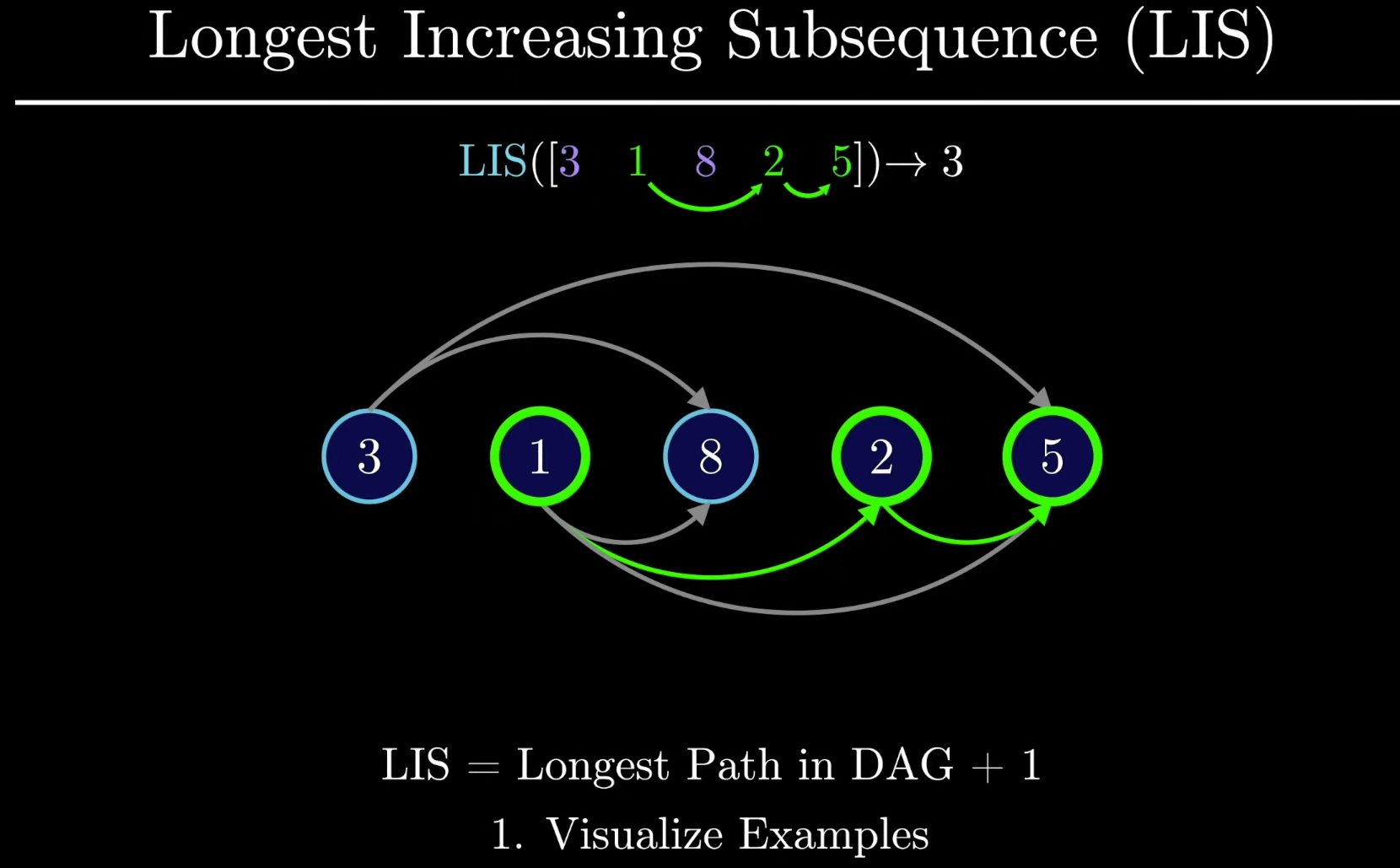
Defining the Subproblem §

Once we have a better understanding of the problem we can start finding an appropriate subproblem. What we know so far is:

• All increasing subsequences are subsets of the original sequence
• All increasing subsequences have a start and end

In this case using the end index may be more intuitive. We can describe our subproblem as: The length of the longest increasing subsequence ending at index K = $LIS[k]$

Therefore

• $LIS[0]=1$
• $LIS[1]=1$
• $LIS[2]=2$
• $LIS[3]=2$
• $LIS[4]=3$

Define the relationship among subproblems §

At this stage it may help to ask yourself what subproblems are necessary to solve the current subproblem?

If we wanted to solve the subproblem $LIS[4]$ then we would need to find the longest increasing subsequences for each directed edge pointing to index 4. In this case it is index {0, 1, 3}. For index 0 there are no incoming edges so the $LIS[0]=1$ For index 1 there are no incoming edges so the $LIS[1]=1$ For index 3 there is one incoming edge so the $LIS[3]=2$

Therefore for $LIS[4]$

$LIS[4]=1+max\{LIS[0],LIS[1],LIS[3]\}=3$

Generalise the relationship Now that we have mapped a relationship for index 4 we can generalise the relationship between subproblem. 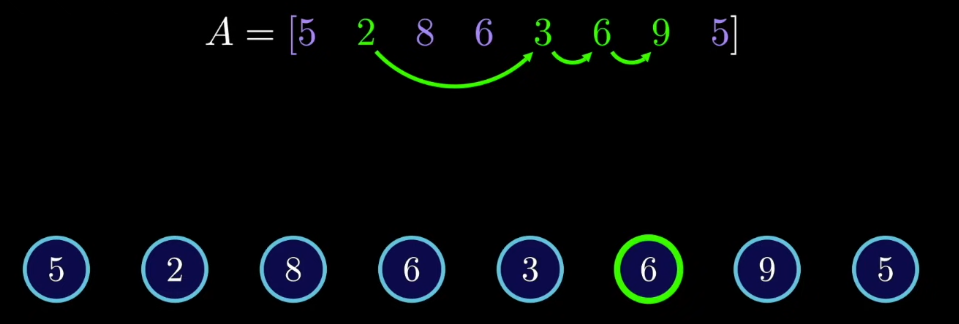If we wanted to solve the subproblem $LIS[5]$ what do we need to consider?

• We can only consider indices less than the current index. So if we want to consider an index $k$ then we need to make sure $k<5$.
• Additionally to be an increasing subsequence, a valid index $k$ must also contain a value smaller than the current index. So $A[k]<A[5]$

We can write the following subproblem as:

$\begin{array}{rl}LIS[5]& =1+\max \{LIS[k]|k<5,A[k]<A[5]\}\\ & =1+\max \{LIS[0],LIS[1],LIS[4]\}\\ & =1+\max \{1,1,2\}\\ & =3\end{array}$

It can be generalised for any index $n$ by swapping 5 for $n$

$LIS[n]=1+max\{LIS[k]|k<5,A[k]<A[n]\}$

Implementation §

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        // Every path has at least length 1, the node itself
        Arrays.fill(dp, 1);
        
        // Iterate over every node
        for (int n = 1; n < nums.length; n++) {
            int maxLength = 0;
            // Search all nodes previous to current nth index
            for (int k = 0; k < n; k++) {
                if (nums[k] < nums[n]) {
                    // Compare paths where value of index k < value of index n
                    maxLength = Math.max(maxLength, dp[k]);
                }
            }
            // Update current maximum length for paths ending at index n
            dp[n] = 1 + maxLength;
        }
        
        // Iterate to find max length path out of all nodes
        int maxLIS = 0;
        for (int num : dp) {
            maxLIS = Math.max(maxLIS, num);
        }
        return maxLIS;
    }
}

Extension §

What if we wanted to find the actual subsequence itself and not just the length? We can create a new array to track the previous index used to create the current $LIS[n]$ For the earlier example, the array was $[3,1,8,2,5]$. Let a node without a previous index = $-1$ Therefore:

• $prev[0]=-1$
• $prev[1]=-1$
• $prev[2]=0$
• $prev[3]=1$
• $prev[4]=3$

Since the largest increasing subsequence ends at index 4, we can iterate through the $prev$ array to get the sequence. Starting at index 4 the previous node is $prev[4]$ which is index 3. At index 3 the previous node, $prev[3]$ would be index 1. Since $prev[1]=-1$, that is where our path began.

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        // Every path has at least length 1, the node itself
        Arrays.fill(dp, 1);
        // Array to track previous index in path
        int[] prev = new int[nums.length];
        Arrays.fill(prev, -1);
 
        for (int n = 1; n < nums.length; n++) {
            int maxLength = 0;
            for (int k = 0; k < n; k++) {
                if (nums[k] < nums[n] && dp[k] > maxLength) {
                    maxLength = dp[k];
                    prev[n] = k;
                }
            }
            dp[n] = 1 + maxLength;
        }
 
        int maxLIS = 0;
        int maxIndex = 0;
        for (int i = 0; i < dp.length; i++) {
            if (dp[i] > maxLIS) {
                maxLIS = dp[i];
                maxIndex = i;
            }
        }
        // Print out the path in reverse order
        System.out.print(nums[maxIndex] + ",");
        while (prev[maxIndex] >= 0) {
            System.out.print(nums[prev[maxIndex]] + ",");
            maxIndex = prev[maxIndex];
        }
        return maxLIS;
    }
 
}

References §

• 5 Simple Steps For Solving Dynamic Programming Problems
• Dynamic Programming - TechParoksha